12. 中心极限定理 [选修]
中心极限定理
从这里开始直到高斯分布课程结尾的内容皆为选修部分。
这一部分介绍了高斯分布的由来。如果你想深入学习高斯分布背后的理论,那么请继续。如果你不想,也可以直接跳到机器人定位课程。
总体
总体中包含了数据集中的所有值。在这一课中,我们将用到的数据就像下面这样:
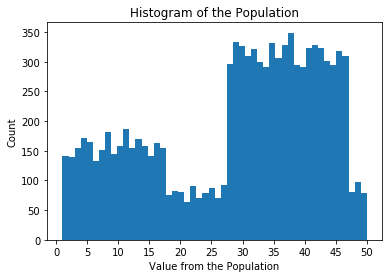
Population Distribution
例如,值 15 在总体中大概出现了 160 次,值 50 在总体中大概出现了 70 次。这个总体中一共有 10,000 个数据点。
随机从这一分布中抽取 100 个数据点,并将这 100 个数据点称为一个样本。接着计算该样本的均值。如果你照此方法反复抽取样本,得到的均值将呈高斯分布。
随着大量样本均值的计算,看着人口分布逐渐向高斯分布靠近,这是一件十分神奇的事。
在本课程的下一部分,我们将为你呈现如何使用 Python 代码做到这一点。